ADN Open CIS
Сообщество программистов Autodesk в СНГ

Плоскости, проекции и выбранные точки

В статье обсудим вопрос и пример кода, касающийся новшеств Revit API, в частности при работе с плоскостями, проекциями и выбранными точками.

Вопрос: В коде, приведенном ниже, я задаю рабочую плоскость на текущем виде и предлагаю пользователю выбрать две точки, для вычисления площади прямоугольника. Код работает для восточного и западного фасада, но на северном и южном фасадах, площадь равна 0. Есть какие-нибудь идеи, почему так может быть? Если же я задаю рабочую плоскость вручную в пользовательском интерфейсе на северном и южном фасадах и выполняю код, в котором вычисляю только площадь без создания рабочей плоскости, то площадь вычисляется нормально.

Также помимо этого, код основывается на координатах XYZ, и не позволяет вычислить правильную площадь, скажем для стены, повернутой на 45 градусов. Как можно сделать мой код более универсальным?

Ответ: Ваш вопрос и код затрагивает кучу проблем и советов. Многие из общего характера.

Использование отладчика

В вашем случае в первую я бы предложил посмотреть на координаты выбранных точек в отладчике.

Возможно проблема сразу станет ясной.

Поместить транзакцию в блок ‘using’

Самый простой и безопасный способ работы с транзакциями в Revit API – заключить каждую транзакцию и группу транзакций в блок ‘using’. В этом случае транзакция автоматически будет уничтожена и выполнен откат транзакции, в случае отсутствия явного подтверждения транзакции.

Команда «Только для чтения»

На самом деле нет необходимости вручную создавать рабочую плоскость исходя из направления вида и его исходной позиции, и затем делать черновую рабочую плоскость по нему. Вид уже имеет встроенную рабочую плоскость, которую мы с легкостью можем использовать.

Создание плоскости необходимо производить в транзакции. А раз в этом нет необходимости, то всю команду можно сделать read-only.

Никогда не сравнивать числа с плавающей запятой с помощью оператора “==”

Вы используете явный оператор сравнения «==» для сравнения выбранных координат.

Я бы рекомендовал никогда так не делать, так как они могу различаться на ничтожно малую величину. В этом случае оператор сравнения вернет «ложь», хотя они координаты практически идентичны c допустимой погрешностью. Нужно использовать неточной сравнение для чисел с плавающей запятой. Взгляните на эту тему – тестирование сравнение чисел с плавающей запятой (на англ.)

Это кстати может быть одной из причин, почему ваш код не работает так как надо.

Используйте класс XYZ вместо отдельных переменных X, Y, Z

Ваш код может стать короче и легче для чтения и понимания, если бы вы использовали класс XYZ, вместо того, чтобы обращаться к 3D координатам X, Y, Z по отдельности.

Например, для вычисления вектора v между двумя заданными точками p1 и p2, можно просто воспользоваться строкой:

v=p2 – p1;

Вычисление расстояния в отдельности между всеми тремя координатами по отдельности и сохранение каждого результата в своей переменной делает код громоздким и сложным для понимания.

Метод выбора точки выбрасывает исключение при отмене

Методы Revit API, которые позволяют пользователю выбирать точки или объекты в модели, выбрасывают исключение, если пользователь отменил операцию выбора.

К сожалению, это совершенно противоречит правилу, что исключения должны возникать лишь действительно в исключительных ситуациях.

Тем не менее, я всегда добавляю конструкцию try-catch при выборе точки или объекта с перехватом исключения Autodesk.Revit.Exceptions.OperationCanceledException. Оно возникает в случае отмены операции и в этом случае имеет смысл возвратить Result.Cancelled или Result.Failed в зависимости от ситуации.

Серьезные предложения по улучшению кода

Главная проблема текущей реализации состоит в том, вы жестко закодировали зависимость рабочей плоскости параллельно основным осям координат, что собственно вы и указали. Этот подход вернет не верный результат, если рабочая плоскость будет наклонена.

Более правильным решением будет проекция двух выбранных точек на рабочую плоскость (так как они выбираются на плане, то они по-любому должны находится на ней) и определить их UV координаты на этой плоскости.

Это даст вам двумерные координаты точек, соответственно вычислить площадь не составит никакого труда.

Вы должны использовать что то типа метода Face.Project, который проецирует XYZ точку на поверхность и возвращает объект типа IntersectionResult, из которого можно получить двумерные координаты точки.

К сожалению, Revit API не содержит такого метода для класса Plane, поэтому нам нужно создать его самостоятельно.

В качестве альтернативного варианта, но немного излишнего и сложного, можно предложить использовать функциональность AutoCAD ARX в Revit.

Там есть метод Geometry.AcGe.Helper.orthoProjectIntoPlane, который делает как раз то, что нам необходимо.

Но, так мне самому нравится делать всякие геометрический вычисления, то я не упущу такой шанс и продемонстрирую как это можно сделать самостоятельно.

Реализация методом расширения

Первым делом я реализовал три вспомогательных метода расширения для класса Plane:

• SignedDistanceTo – вычисляет расстояние от рабочей плоскости до заданной точки

• ProjectOnto – проецирует заданную трехмерную точку на рабочую плоскость

• ProjetInto - проецирует заданную трехмерную точку на рабочую плоскость и возвращает двумерные координаты в координатной системе плоскости

Для реализации методов расширения, нужно создать статический класс со статическим методом, принимающем в качестве параметра указатель на класс, который вы расширяете с ключевым словом ‘this’. В моем случае, я добавил класс JtPlaneExtensionMethods  в файл Util.cs в примеры The Building Coder.

Математическое определение плоскости и определение плоскости в Revit

Плоскость может быть определена четырьмя числами. Три из них задают нормаль и четвертая является расстоянием до начала координат.

Плоскости в Revit немного более сложные. В том плане, что они задаются с помощью начальной точки и двумя векторами X и Y, которые определяют направление двумерных координатных осей.

Следовательно, в трёхмерную рабочую плоскость уже встроена двумерная система координат.

Расстояние от трёхмерной точки до плоскости

Вычисление расстояние осуществляется с помощью скалярного произведения.

Что же такое скалярное произведение?

Геометрически это можно представить себе, как длина проецирования одного вектора на другой:

 

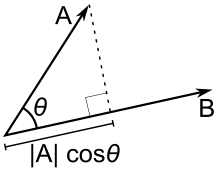
Используя его, вычислить расстояние от точки до плоскости не составит труда. Определите вектор между заданной точкой и произвольной точкой на плоскости. Скалярное произведение между этим вектором и вектором нормали плоскости и будет являться расстоянием от точки до плоскости.

Вот моя реализация этого алгоритма:

Проекция трехмерной точки на поверхность

Метод ProjectOnto возвращает трехмерную точку, представляющую собой проекцию заданной точки в пространство на поверхности плоскости. Результат легко посчитать, вычитав произведение вектора нормали плоскости на расстояние до точки из координат заданной точки:

Проекция трехмерной точки внутрь поверхности

Проецирование внутрь поверхности похоже на проецирование на поверхность. Но вместо трехмерной точки метод возвращает двумерную точку, представляющую собой точку в локальной двумерной системе координат заданной поверхности.

Иными словами, трехмерная точка, полученная с помощью метода ProjectOnto возвращает трехмерные координаты глобальной системы координат. Двумерная же точка принадлежит системе координат поверхности.

Ее можно вычислить с помощью скалярного произведения вектора между исходной точкой поверхности и проецированной точкой с векторами X и Y соответственно. Эти два вектора определяют направление координатных осей U и V на поверхности плоскости:

Выбранные точки для вычисления площади

С помощью этих вспомогательных методов можно реализовать ваш метод SetWorkPlaneAndPickPointsForArea например вот так (я переименовал его в PickPointsForArea, так как создавать поверхность больше не нужно):

Обновленные примеры

Приведенный выше код я добавил в примеры The Building Coder.

Как всегда, вы их можете скачать на GitHub. Версия примеров, обсуждаемая в статье – 2015.0.111.2

Если же вы не хотите качать целиком все примеры, то вот прямые ссылки на классы Util и CmdPickPoint3d.

Источник: http://thebuildingcoder.typepad.com/blog/2014/09/planes-projections-and-picking-points.html